亲爱的游戏迷们,你是否曾在某个午后,无聊地摆弄着手机,突然被一款小游戏深深吸引?没错,我说的就是那款让人又爱又恨的扫雷游戏!今天,我要带你深入探索这款游戏的奥秘,揭秘它背后的递归算法,让你在轻松愉快的氛围中,领略编程的魅力。
想象你面前是一张布满数字和问号的棋盘,你的任务是找出所有的雷,同时避免踩到它们。看似简单,但当你真正开始玩的时候,你会发现,这不仅仅是一款游戏,更是一种挑战。

那么,这款小游戏是如何实现的呢?答案就是递归算法。递归,顾名思义,就是函数自己调用自己。在扫雷游戏中,递归算法的作用是,当你点击一个格子时,程序会自动判断这个格子周围是否有雷,如果有,就标记出来;如果没有,就继续递归判断周围的其他格子。
递归算法的核心在于递归终止条件。在扫雷游戏中,递归终止条件有两个:
1. 当你点击的格子是雷时,游戏结束。
2. 当你点击的格子不是雷,且周围没有雷时,游戏胜利。
这两个条件保证了递归算法的正确性和有效性。
下面是一个简单的递归算法实现示例:
```c
void findMine(char mine[ROWS][COLS], char show[ROWS][COLS], int row, int col) {
// 判断是否越界
if (row < 0 || row >= ROWS || col < 0 || col >= COLS) {
return;
}
// 判断是否是雷
if (mine[row][col] == 'R') {
show[row][col] = 'R';
return;
}
// 判断周围是否有雷
int count = 0;
for (int i = -1; i <= 1; i++) {
for (int j = -1; j <= 1; j++) {
if (mine[row + i][col + j] == 'R') {
count++;
}
}
}
// 标记数字
show[row][col] = '0' + count;
// 递归判断周围的其他格子
for (int i = -1; i <= 1; i++) {
for (int j = -1; j <= 1; j++) {
findMine(mine, show, row + i, col + j);
}
}
这段代码实现了递归判断周围格子的功能。当你点击一个格子时,程序会调用这个函数,然后根据递归终止条件,逐步判断周围的其他格子。
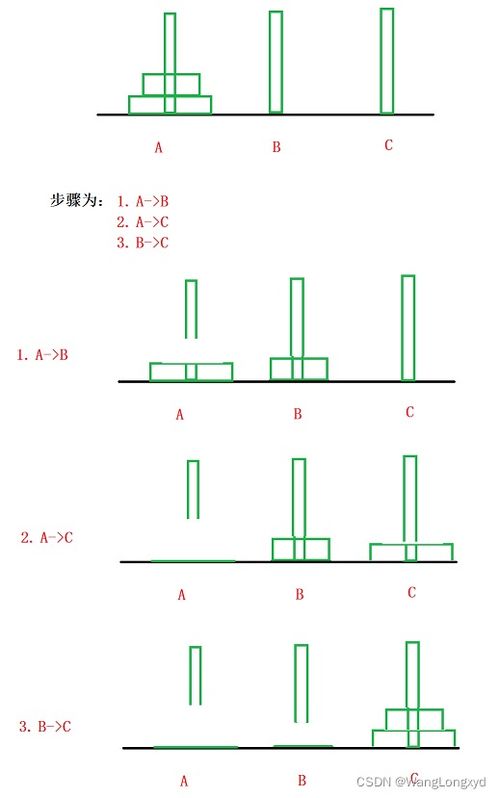
递归算法不仅仅应用于扫雷游戏,它在现实生活中的应用也非常广泛。比如,著名的汉诺塔问题、搜索算法等,都离不开递归算法。
通过本文的介绍,相信你已经对递归算法有了更深入的了解。递归算法让扫雷游戏变得更加有趣,也让我们的生活变得更加丰富多彩。让我们一起,用递归算法创造更多精彩的游戏吧!